Travaux pratiques : Présentation de l'EEA
DEUG A, 1ère année.

Réalisation d'un correcteur PI à l'aide de montages
utilisant un amplificateur opérationnel.

3ème séance.

1. Electronique analogique fonctionnelle.

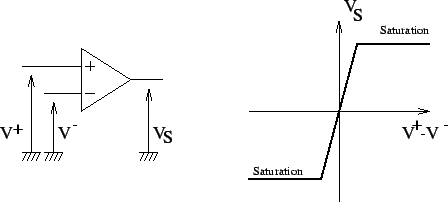
L'amplificateur opérationnel (AOP) possède une caractéristique statique indiquée sur la figure (1).

Figure: Symbole et caractéristique statique d'un amplificateur opérationnel.
\includegraphics {AOP.eps}

Le gain statique \( A_{D} \) de ce système est égal à \( 10^{5} \) environ. Dans son domaine de fonctionnement linéaire, on peut écrire :


\begin{displaymath} V_{S}=A_{D}\cdot (V^{+}-V^{-})\end{displaymath}

Par la suite, l'AOP sera considéré parfait ce qui revient à prendre les hypothèses suivantes:

Dans ces conditions, un bouclage sur l'entrée - (inverseuse) conduit à la relation :


\begin{displaymath} V^{+}=V^{-}\end{displaymath}

Cette condition correspond à une erreur statique nulle ce qui a déjà été remarqué dans le cas d'un asservissement avec un correcteur proportionnel à gain infini.

L'AOP permet de réaliser différents montages fonctionnels. Nous nous limiterons aux cas suivants :

Ils seront réalisés à l'aide d'une platine d'expérimentation. Elle devra être alimentée en imposant -15V, 0, +15V.

1.1 Montage amplificateur inverseur.

Le schéma est donné sur la figure (2).

Figure 2: Montage amplificateur inverseur.
\includegraphics {ampli.eps}

1.1.1 Etude théorique.

Calculer la valeur théorique du gain \( G=V_{S}/V_{E} \).


\begin{displaymath} G=\end{displaymath}

1.1.2 Etude expérimentale.

Réaliser le montage avec \( R_{1}=10k\Omega \), la résistance \( R_{2} \) est matérialisée par une résistance variable (boîte de résistances).

Appliquer pour \( V_{E} \) une tension sinusoïdale de fréquence f=1kHz et d'amplitude crête 3V (soit crête-crête 6V).

Mesurer la valeur de ce signal au voltmètre. Expliquer l'écart.

Observer à l'oscilloscope les tensions d'entrée et de sortie pour 3 valeurs de la résistance \( R_{2} \)=\( 10k\Omega , \) \( 20k\Omega \) et \( 50k\Omega \).

1.2 Montage additionneur.

Le schéma est donné sur la figure (3).

Figure 3: Montage additionneur.
\includegraphics {additionneur.eps}

1.2.1 Etude théorique.

Calculer la valeur théorique de la tension \( V_{S} \).


\begin{displaymath} V_{S}=\end{displaymath}

A quelle condition peut-on écrire : \( V_{S}=-5V_{1}-V_{1}^{'} \)

On choisit une tension \( V_{1}^{'} \) sinusoïdale de fréquence 1kHz et d'amplitude crête 1V et une tension \( V_{1}^{'} \) continue égale à +5V. Ecrire l'équation de la tension de sortie en fonction du temps.

1.2.2 Etude expérimentale.

Les 2 résistances \( R_{1} \) et tex2html_wrap_inline153 sont des résistances variables et la résistance \( R_{f} \) est égale à \( 10k\Omega \). Réaliser le montage correspondant aux 2 dernières questions de l'étude théorique et comparer les résultats théoriques et expérimentaux. Conclusions.

1.3 Montage soustracteur.

Le schéma est donné sur la figure (4).

Figure 4: Montage soustracteur.
\includegraphics {soustract.eps}

1.3.1 Etude théorique.

Calculer la valeur théorique de la tension \( V_{S} \).


\begin{displaymath} V_{S}=\end{displaymath}

Quelle est la condition sur les résistances \( R_{1} \), \( R_{2} \), \( R_{p} \) et \( R_{f} \) permettant d'écrire \( V_{S}=A\cdot (V_{2}-V_{1}) \). Donner dans ces conditions l'expression du gain A.

A quoi peut servir ce montage ?

1.3.2 Etude expérimentale.

Les 2 résistances \( R_{p} \) et \( R_{f} \) sont des résistances variables et les résistances \( R_{2} \) et \( R_{1} \) sont égales à \( 10k\Omega \).

Réaliser un montage permettant d'obtenir successivement A=1, 2 et 3. Vérifier son fonctionnement pour \( V_{2} \) un signal TTL de fréquence 1kHz et \( V_{1} \) une tension continue égale à 2.5V.

1.4 Montage intégrateur.

Réaliser le montage indiqué sur la figure (5).

Figure: Montage pseudo-intégrateur.
\includegraphics {integr.eps}

Vérifier son fonctionnement avec une tension d'entrée successivement carrée, triangulaire et sinusoïdale. Prendre les valeurs suivantes de composants:

2. Réalisation d'un asservissement PI en utilisant les montages électroniques précédents.

L'utilisation d'un correcteur proportionnel entraîne l'oscillation de la sortie de l'aérotherme pour des gains élevés du correcteur. On se propose de réaliser un correcteur PI pour asservir correctement l'aérotherme. On utilisera le montage indiqué sur la figure (6).

Figure: Montage utilisé pour l'asservissement PI.
\includegraphics {PI.eps}

2.1 Etude théorique.

Exprimer \( V_{s} \) en fonction de \( A\cdot \epsilon \).

En déduire la valeur de \( \epsilon \) pour laquelle la tension \( V_{s} \) est une constante. Quelle est la relation qui relie alors la consigne à la sortie? Le résultat dépend-il du gain?

2.2 Etude expérimentale.

Réaliser le montage pour \( R_{1}=R_{2}=10k\Omega \), \( R=6.8M\Omega \) et \( C=1\mu F \). Les 2 résistances \( R_{p} \) et \( R_{f} \) sont des résistances variables que l'on ajustera pour obtenir successivement A=1, 2 et 5.

Vérifier le fonctionnement de l'asservissement.

Etudier l'influence du gain A sur la réponse dynamique du système.

À propos de ce document...

Travaux pratiques : Présentation de l'EEA
DEUG A, 1ère année.

This document was generated using the LaTeX2HTML translator Version 99.1 release (March 30, 1999)

Copyright © 1993, 1994, 1995, 1996,

Routoure JM
2001-09-04